Comic Strips

18697 readers

1890 users here now

Comic Strips is a community for those who love comic stories.

The rules are simple:

The post can be a single image, an image gallery, or a link to a specific comic hosted on another site (the author's website, for instance).
The comic must be a complete story.
If it is an external link, it must be to a specific story, not to the root of the site.
You may post comics from others or your own.
If you are posting a comic of your own, a maximum of one per week is allowed (I know, your comics are great, but this rule helps avoid spam).
The comic can be in any language, but if it's not in English, OP must include an English translation in the post's 'body' field (note: you don't need to select a specific language when posting a comic).
Politeness.
AI-generated comics aren't allowed.
Adult content is not allowed. This community aims to be fun for people of all ages.

Web of links

!linuxmemes@lemmy.world: "I use Arch btw"
!memes@lemmy.world: memes (you don't say!)

founded 2 years ago

MODERATORS

lawrence@lemmy.world

511

Zeno's Dichotomy Paradox (sh.itjust.works)

submitted 1 year ago by otter_band@sh.itjust.works to c/comicstrips@lemmy.world

23 comments fedilink hide all child comments

Zeno's Dichotomy Paradox

you are viewing a single comment's thread
view the rest of the comments

[–] NeatNit@discuss.tchncs.de 12 points 1 year ago (1 children)

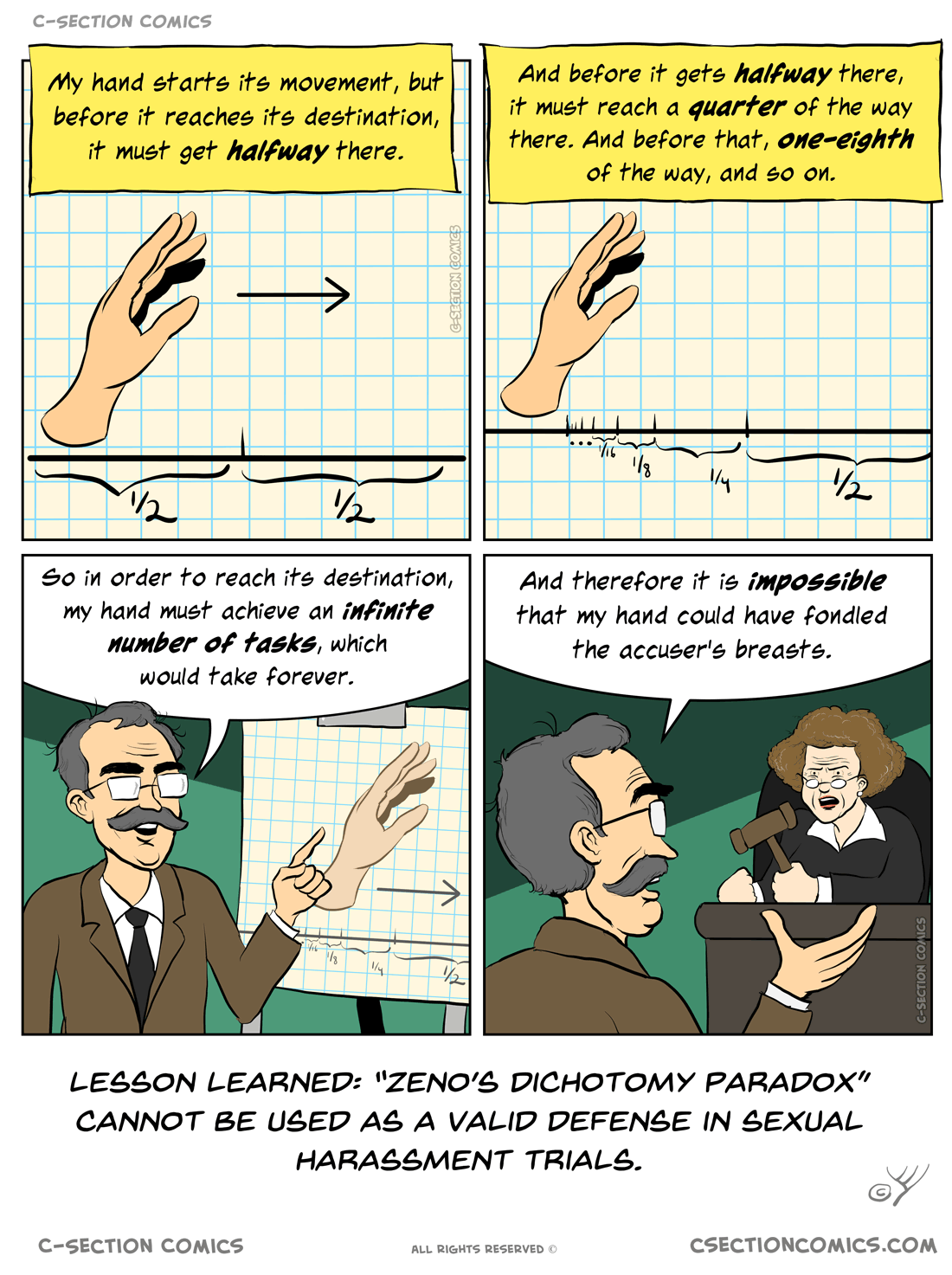
I think this idea works, and it's consistent with the way the 'paradox' was presented. I just need to point out that movements aren't performed in steps, the intermediate positions are also continuous, so there are undoubtedly infinite positions to map with undoubtedly infinite instants. To me, that's the "true" solution.

As I see it, the only reason the paradox presents halving steps is because it's the easiest way to demonstrate that there are infinitely many steps. It doesn't bother to show that there's uncountably infinite steps because countable is sufficient.

But as I said, your proof (or disproof?) works for the argument as it was presented, so it's good!

I much prefer the physics approach: disproof by experiment! "Look at my gavel. According to your theory, it has infinitely many steps to go through before it reaches the pad, so it can never hit the pad." *bang* "Motion denied."